
 |
|
Da Lichtwellen elektromagnetische Wellen sind und das aus den Maxwellschen Gleichungen folgende Prinzip der linearen Superposition gilt, breitet sich jede Welle ungestört von weiteren Wellen aus.
Überlagert man zwei elektromagnetische Wellen derselben Frequenz
n = w / 2
p, die sich beide in Richtung ![]() fortpflanzen, ergibt sich die Feldstärke E der Gesamtwelle mit
fortpflanzen, ergibt sich die Feldstärke E der Gesamtwelle mit
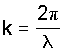 ( 3-2 )
( 3-2 )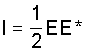 ( 3-3 ),
( 3-3 ),Ändert sich die Phasendifferenz ![]() statistisch, so treten keine Interferenzerscheinungen mehr auf. Die zeitliche
Änderung der Phase bestimmt somit die zeitliche Kohärenz. Nur
fiktive monochromatische Lichtquellen mit einer Frequenzbandbreite von
statistisch, so treten keine Interferenzerscheinungen mehr auf. Die zeitliche
Änderung der Phase bestimmt somit die zeitliche Kohärenz. Nur
fiktive monochromatische Lichtquellen mit einer Frequenzbandbreite von ![]() sind zeitlich völlig kohärent. Die Kohärenzzeit D
t, der zeitliche Bereich während dessen eine Lichtquelle konstante
Phasenbeziehungen besitzt, läßt sich als Kehrwert der Frequenzbandbreite
darstellen:
sind zeitlich völlig kohärent. Die Kohärenzzeit D
t, der zeitliche Bereich während dessen eine Lichtquelle konstante
Phasenbeziehungen besitzt, läßt sich als Kehrwert der Frequenzbandbreite
darstellen:
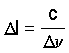 ( 3-7 ).
( 3-7 ).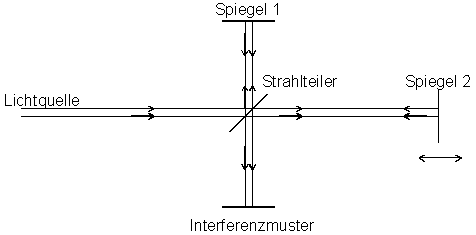
Das Licht einer Quelle wird durch einen Strahlteiler getrennt und fällt auf die Spiegel 1 und 2. Es wird reflektiert und durch den Strahlteiler wieder vereinigt, um auf einen Schirm aufzutreffen. Auf diesem wird nur dann ein Interferenzbild – Abbildung 1-4 – erzeugt, wenn der Wegunterschied der beiden Teilbündel nicht größer als die Kohärenzlänge ist. Wird durch Verschieben eines der beiden Spiegel der Wegunterschied verändert, so ergeben sich aufeinanderfolgende Maxima bei Wegunterschieden von
Inhomogenitäten der Spiegel oder des Strahlteilers machen sich als Irregularitäten in den Interferenzmustern bemerkbar, worauf viele Anwendungen beruhen.In ähnlicher Weise – durch den Youngschen Versuch – kann die räumliche
Kohärenz definiert werden.
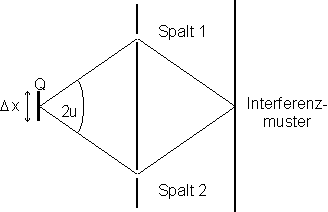
Eine monochromatische Lichtquelle Q mit der endlichen Ausdehnung D x und dem Öffnungswinkel 2u beleuchtet einen Doppelspalt. Die von den beiden Spalten ausgehenden Wellen interferieren, wenn beide eine definierte Phase besitzen. Hierfür läßt sich die Grenzbedingung
| Für Anmerkungen oder Änderungen senden Sie ein e-mail an martin@martin-mandl.com 980402 |